Emergence and Chaos in Games

In my previous article “Systemic Information in Games”, I put forward the idea that the key feature of games is that they are systems and that they therefore provide opportunities for systemic learning. Systemic learning refers to the acquisition of information about a system, and the use of this information in creating mental models with predictive power, upon which we can base decisions. Our decisions within a game are simply predictions about which actions are most likely to lead to victory. This is true regardless of our level of certainty and the method we have used to arrive at that decision. All non-random systems are perfectly predictable in theory, but the properties of a given system will affect how predictable it is in practice and which kinds of methods are best suited to predicting it.

Just like games, science is largely about understanding and predicting systems, so it stands to reason that ideas and concepts from science will have useful applications in the realm of game design. Here I want to relate two concepts from science, which will hopefully help us to think more clearly about this fairly abstract domain. These concepts are emergence and chaos.

Emergence
Any complex system, meaning any system with multiple elements that interact with each other, will produce emergent behaviours. With games, as with the real world, the vast majority of information we end up learning is about these emergent properties.

But to start at the beginning, what is a game by the simplest description? A game is a collection of rules and elements. Elements are constrained by rules. These elements are like the atoms of our universe, rules are like the physical laws that constrain the atoms. Just as there are different types of atoms, there are a variety of possible game elements – cards, pieces, characters, resources. The game state is a snapshot of all of the elements at a given point in time. The rules therefore define and limit how the state of the game can change over time. To illustrate, two possible game states in chess, identical but for a single pawn moved three squares across the board, cannot be directly linked because the game rules do not allow a pawn to move three squares in one turn. That transformation is not allowed. This game state can, however, be reached in multiple transformations.

This is an illegal transformation, the movement of the pawn breaks the rules of the game, and so these states are not directly connected to each other

This state can be reached in multiple moves, so these board states are connected indirectly

And here we see the first hint of emergence. The rules define which state transformations are impossible, but they do not directly define which states are impossible. However, because of the rules, some game states are impossible, as illegal transformations would be required to reach them. So there is no rule which says a mirrored version of the starting board state is not allowed in chess, but a result of the rules, which limit how elements can change over time, is that such a state cannot be reached. This is an emergent property, a result of the interactions of the rules and which is not in itself a rule.

There is no sequence of transformations that can get you from the first board state to the second, as pawns cannot move past one another without capturing pieces
The second board state is therefore not present in the entire possibility space of chess

Alternatively, instead of describing a game as a set of rules and elements, it is possible to describe a game as a particular possibility space, a network of game states connected by possible transformations. This definition does not appeal to me however, because it is too abstract. Thinking about games in this way has little obvious utility for designers, and it disagrees with our intuitive perception of games, which is that the possibility space emerges from the rules rather than the other way around. It may have value for drawing deeper conclusions about the properties of games, however at the present my intuition is that it is something of a dead end. Useful abstract notions like emergence vanish in this perspective, and so it becomes difficult to draw conclusions which have any relevance to humans.

The Emergence Stack
One way to think about emergence is using the real world as an example. The real world is a system, just like a game. We can imagine each of the scales we think about when considering the physical universe as a layer in a stack.

Each of these layers is built upon the one below it, and each is listed above by its elements, rather than its governing rules. We can create a similar stack for rules instead –

We might imagine that there are analogous stacks that represent the emergent properties of a game –

In reality, such a stack would be much more vague and ambiguous than the stack describing reality, the layers may be less distinct from one another. Again, the purpose of having these multiple levels is to address phenomena that occur at different scales, the levels of the stack we create to understand a game will be based more on utility than purely based on emergent properties. And there is a clear explanation why this should be the case:

Limited Information and Limited Computation
Emergence is not a concept recognised by the universe as far as I can tell. It is a concept which describes human thought rather than objective fact. It is primarily a result of the way in which we chunk up systems in order to understand them. Emergent properties are simply descriptions of the net result of numerous interactions between the basic elements of a system. The most complete knowledge of a system contains the complete data about each of its lowest level elements and the laws that govern them. With this knowledge there would be no need to invoke emergent properties. Emergence is, however, recognised by humans, because of its utility. Humans operate at a certain scale and within certain computational constraints. We must necessarily compress information we receive about the world and make predictions based on greatly simplified models.

And so the emergence stacks shown above do not represent objective delineations of phenomena in the universe, rather they represent mental models addressing different scales. The physical emergence stack represents a collection of shared mental models, which perhaps appear objective simply because they are generally agreed upon.

The universe, with its limitless computational capacity, understands gravitation and electromagnetism, we limited humans understand that objects fall towards the ground but cannot pass through it. Our understanding is not more complete, in fact is far less complete, but it represents a form of inaccurate information that is never the less far more useful and coherent to us. Given infinite computational power, there is no need for notions of emergence, everything can be understood and predicted based on the laws that govern the most fundamental elements of a system. Given infinite computational power, any higher level understanding of emergent phenomena is strictly inferior to the most basic understanding of the fundamental laws. Descriptions of emergent properties are necessarily less complete than a full description of the system from which the emergent properties arise. Descriptions of emergent phenomena are only useful because of limited computational power, limited information, or limited time.

To relate to games, we can very quickly learn to play chess. The rules of the game are quite simple. And yet master chess players spend years constantly uncovering new things about the game. What does this mean? They are not learning new information about the rules, instead they are learning new abstractions to render the game into a human parsable format, and then refining and improving those abstractions. The rules of the game provide a complete understanding of the game, but this complete understanding does not help us to win when we are simple apes working within narrow computational constraints. Even chess playing computers have to resort to some level of abstraction or simplification due to their limited computational capacity.

The perfect chess player would not use any abstractions, they would understand only the basic rules of chess and would then apply a huge amount of computational power to the task of finding the right move. Humans instead understand positioning, sacrifices, tempo. Things which only roughly describe the state and evolution of the game, but which act as useful forms of compression. With this compression players try to get the maximum utility from the minimum amount of computation. Internally, we might have a kind of mental model of chess defined only by its basic rules. This will be the most accurate mental model we can make, but will be the least efficient because it leaves all of the computation still to be done. More abstract and specific mental models will remove some amount of computational cost. Instead of choosing between moves by looking at the entire network of possible moves that follow, we can choose between them based on notions of good defense, of threatening, of strong or weak formations.

However, none of these “deeper” understandings of chess can help you against the infinite chess computer. Further, an infinite computer using high level emergent knowledge of chess will lose to an infinite computer using knowledge of only the basic rules of chess. Emergent knowledge can never be one hundred percent accurate unless it ceases to be emergent knowledge and reverts back to raw calculation. From this we can see that the utility of mental models, and ideas of emergence in general, comes from reducing our reliance on calculation. In the case of systems like chess, where calculation really can’t get us that far due to our limited mental abilities, mental models can provide some long range predictive power.

Now that we know that emergence stacks are really just mental model stacks, we can see that the layers of a mental model stack for chess would be based less on emergent properties, and more on degree of abstraction and scale. So a revised mental model stack might be a little more like this –

Although with many more layers, and a bit of intermingling between layers. But you might wonder why chess would produce so many layers of mental models in the minds of its players? Are players not able to achieve success with fewer models? And that leads us into the next topic:

Chaos
Another property of complex systems is chaos. This roughly refers to how much of an effect small variations in starting values have on the evolution of the state of a system. A good illustration of this concept is gravity. If we have a system with two celestial bodies orbiting each other, their motions are very stable. Small variations in initial velocity and position will affect the motion, but not greatly, and we can easily predict the state of the system at any point in the future with some equations. This system is highly predictable, and the equations which describe the evolution of the system represent an extreme form of compression. This system is not chaotic.

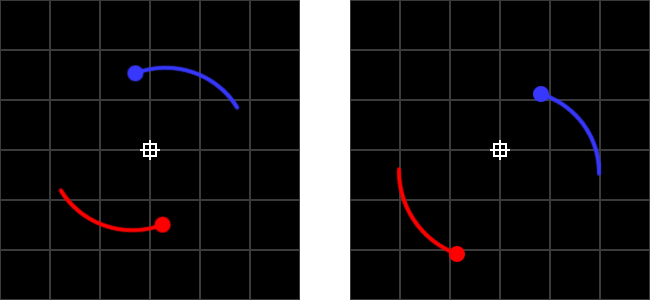This is a two body system at T=10,000. In the left image the initial velocities and positions of the bodies were perfectly mirrored, in the right image the initial velocity of the red body was increased by 5%. This change created an elliptical, but still perfectly stable and predictable orbit

A system containing three bodies however, is highly chaotic. There are no general equations to predict the state of such a system. The slightest variation in the initial state will lead to an entirely different final state. The only way to predict the state of the system at a given time is to walk through the entire evolution of the system leading up to that time. For a three body system the state of the system at any given moment is dependent not only on the starting values, but on the state at every earlier moment. So in a sense, how chaotic a system is determines how much its present state is determined by its previous state as opposed to its initial state.

This is a three body system at T=10,000. The initial velocities and positions of the bodies are perfectly balanced here.

Here the initial velocity of the red body was increased by 5%

Here the initial velocity of the red body was increased by a further 0.001% from the above image. This demonstrates how much even the tiniest variation in starting conditions can affect the system.

It is important to note that, despite what this example may imply, the defining feature of chaotic systems is not how many elements are present, but how many interactions occur and how much they feed into each other. It is possible for a system with only 2 elements to be highly chaotic, but more interactions between the elements would be necessary.

Emergent systems with very low chaos will be relatively predictable based on a single model of their behaviour. Essentially, there will be little information lost when compressing the details of the system into a simplified model. Rendering a more chaotic system into a simplified model will result in more loss of information, and therefore more inaccuracy in predictions based on such a model. Higher amounts of chaos produces more exceptions to any high level generalisations we can make about a system. Because of this, the more chaotic a game is, the more we have to rely on multiple mental models to capture the details. Again, in theory we need only the lowest level of understanding and infinite computational power to have perfect predictive power, but in practice complex emergent systems cause us to employ at least one additional mental model to cut down on calculation, and chaotic emergent systems cause us to use multiple mental models to reduce the inaccuracies that result from any single model. Additional calculation can be used to further reduce errors from model inaccuracies, indeed this is how high level chess players operate, they generate potential moves very quickly in a rather intuitive way, and then spend much longer simulating the game to check whether or not their intuitions have produced inaccurate predictions.

There is of course a limit to the level of chaos we really want in a game system. At a certain point too much chaos will result in a system that is totally impenetrable to beginners, and further beyond that the number of mental models required to make predictions with any useful accuracy will become impractically large, and relying on raw calculation will be the only possible approach, even though humans are totally unsuited to it. The other issue that I have avoided mentioning until now is memorisation. Memorisation is another tool besides mental models for reducing reliance on calculation. Memorisation represents sections of game states, or sequences of moves, which have been shown to be either desirable or undesireable, either through extensive calculation or statistics. High level chess is very heavy on memorisation. Chess openings are a good illustration of this, over the vast number of chess games that have been played, players have accumulated a lot of knowledge about which openings are strong or weak, and which openings are strong against which.

There are multiple factors that contribute to the importance of memorisation in chess, at least one of which is how highly chaotic it is. As discussed earlier, chaos reduces our ability to make long range predictions based on simplified models. As the general complexity of chess is quite high, this weakening of one tool for reducing calculation – mental models, forces us to rely more on an alternate tool for reducing calculation – memorisation. So there is a kind of tension here, chaos is good for increasing the number of mental models that we use, and therefore offers a lot of opportunities for systemic learning, but it also increases the usefulness of memorisation, which is mostly surface learning. Too little chaos and the role of memorisation is far less important, but fewer mental models are needed, and therefore less systemic learning. Less chaos also increases the possibility of degenerate strategies emerging, single tools that solve all problems to a reasonable accuracy. I don’t know that there is a perfect solution, or a perfect balance to be struck, but this is something to keep in mind as a designer.

notes:
Chess board images taken from lichess  – https://en.lichess.org/editor

Here is a neat analysis of some end game chess board states, showing that chess is chaotic – https://www.youtube.com/watch?v=-iEiRMgqBcw

The concept of an emergence stack is similar to the concept of integrative levels – https://en.wikipedia.org/wiki/Integrative_level